Compressive Sensing，CS）方法，该方法正是通过强化稀疏性约束来消除孪生像。最后，他们通过仿真和实验结果验证了该方法的可行性，并与现有的相位检索方法进行了对比。

具体来说，由于图像传感器只对光的强度有响应，因而共轭波U(x,y)作为副产物也被记录下来：当全息图被重构波激活时，“冻结”的波前将继续传播，形成了原始图像；与此同时，相位共轭波前也将被激活并继续传播。虚像平面上的重构是原始图像和孪生像的叠加结果，而共轭情形则出现在实像平面上。因此，全息图重构主要是波的传播问题，而不是透射重构问题。曹教授等人利用在正则基（canonical basis）规范，使得波传播的傅立叶变换特性自然地满足CS的非相干条件：在与距离相关的传播核函数（kernel function）中，物体波衍射成清晰的图案，而相位共轭波衍射成漫散射图案（diffuse pattern）。他们采用全变量稀疏约束（atotal variation sparsity constraint）的迭代算法，滤除了漫反射共轭信号，并克服了全息重构的固有物理对称性。这种方法不受电磁波长、波前形状或支撑约束（support constraints）的限制，适用于绝大多数的自然界物体。

利用压缩传感来消除全息图中的孪生像具有自洽性，不仅抗噪能力强，而且还可以增强CS方法从根本上提升去噪能力。CS作为一种强大的数学工具，已经应用于各种具有重大突破的物理领域，例如更快的STORM、量子态断层扫描、有效的量子动力学测量、预测灾难非线性动力系统，以及互补可观测量。

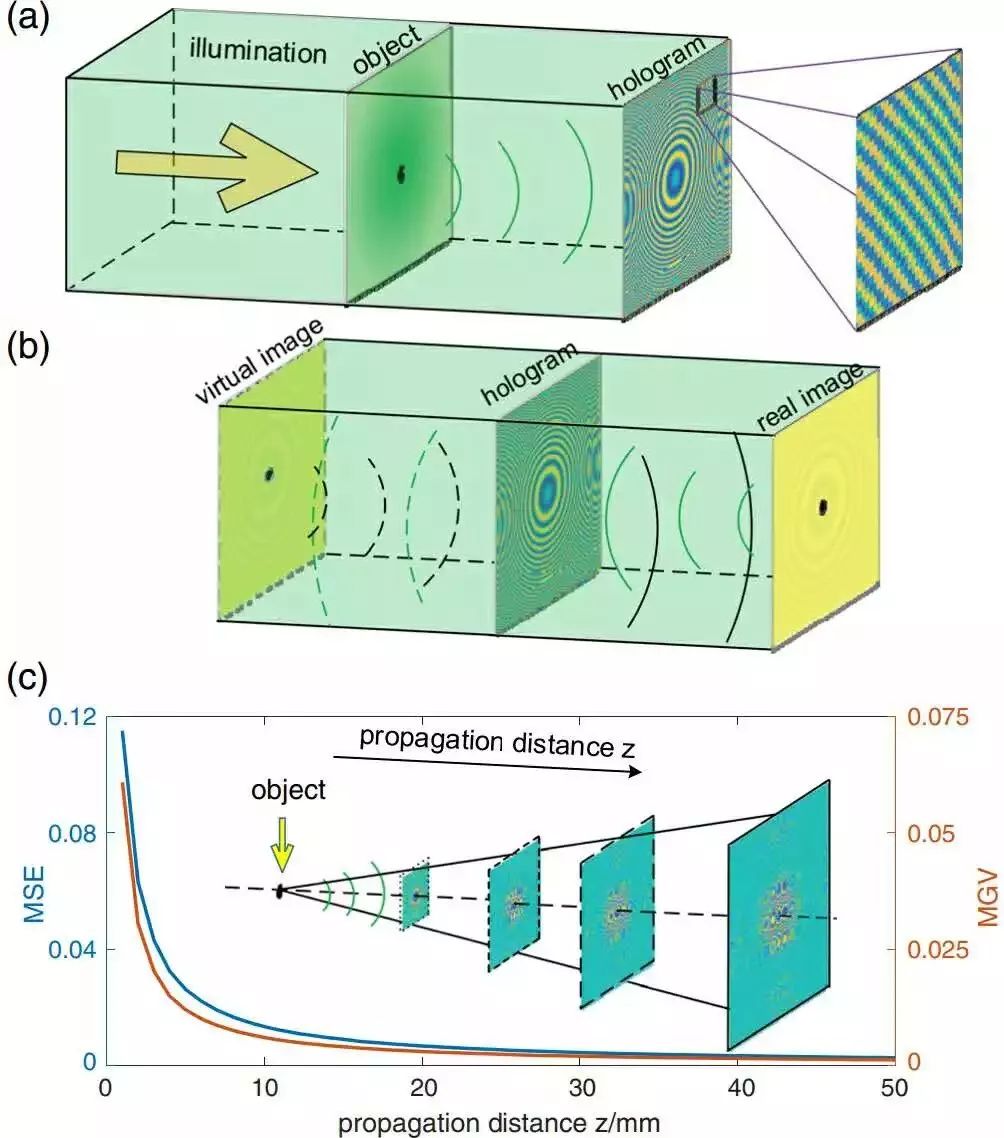
（a）内联菲涅耳（inline Fresnel）全息技术的装置示意。

（b）由于重构期间的波前传播，导致对焦图像和离焦图像的叠加。

（c）在均方误差（MSE）和平均梯度值（MGV）评估下，随着传播距离减小，孪生像对重构的影响效果增大。

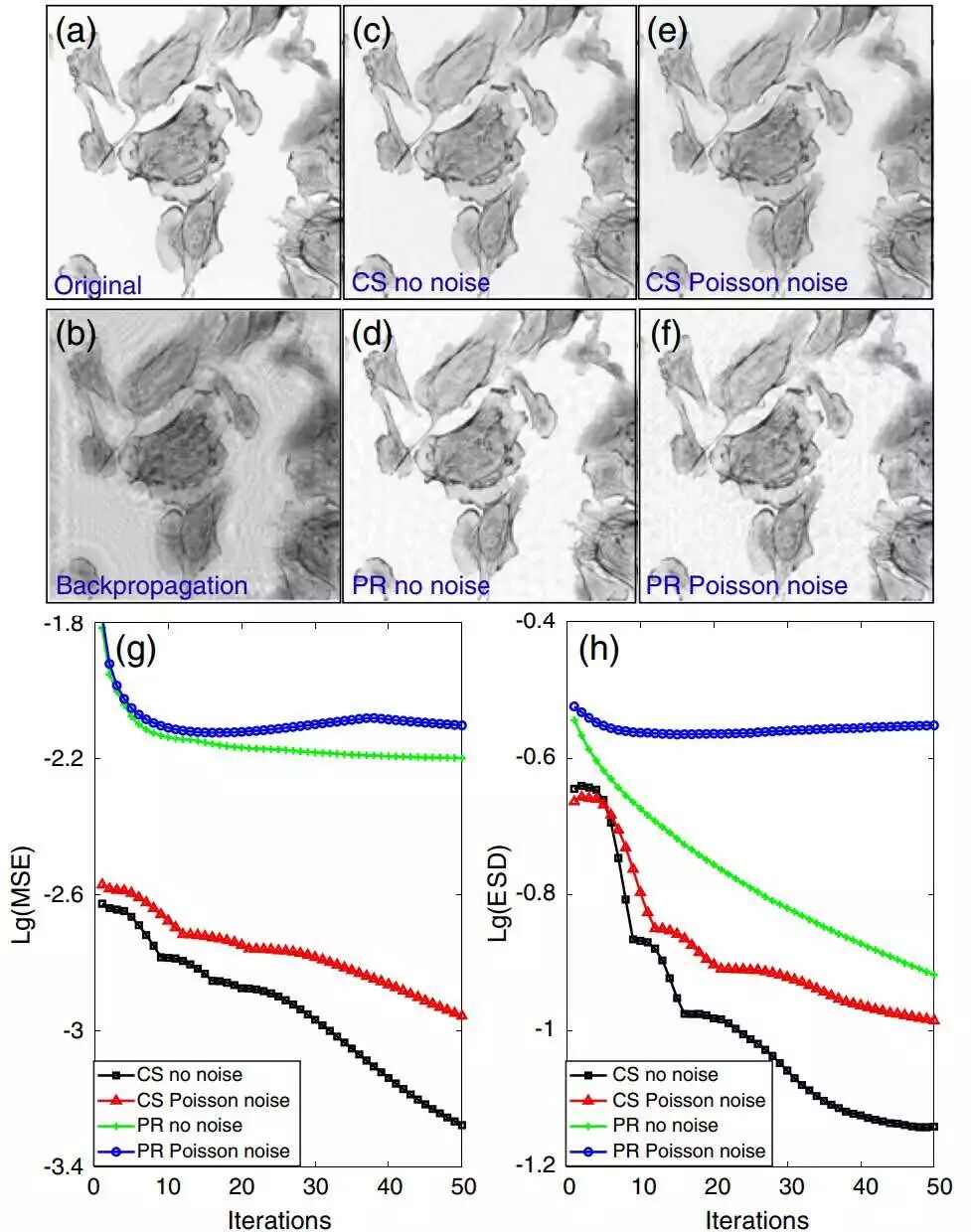
（a）原始图像；

（b）孪生像的反向传播重构；

（c,d）经过50次迭代后,通过压缩传感(CS)和相位检索(PR)从无噪声全息图中的重构；

（e,f）在50次迭代后通过CS和PR从泊松分布噪声全息图重构；

（g,h）lg(MSE)和lg(ESD)的曲线随迭代次数的变化。ESD:边缘稀疏性差异。

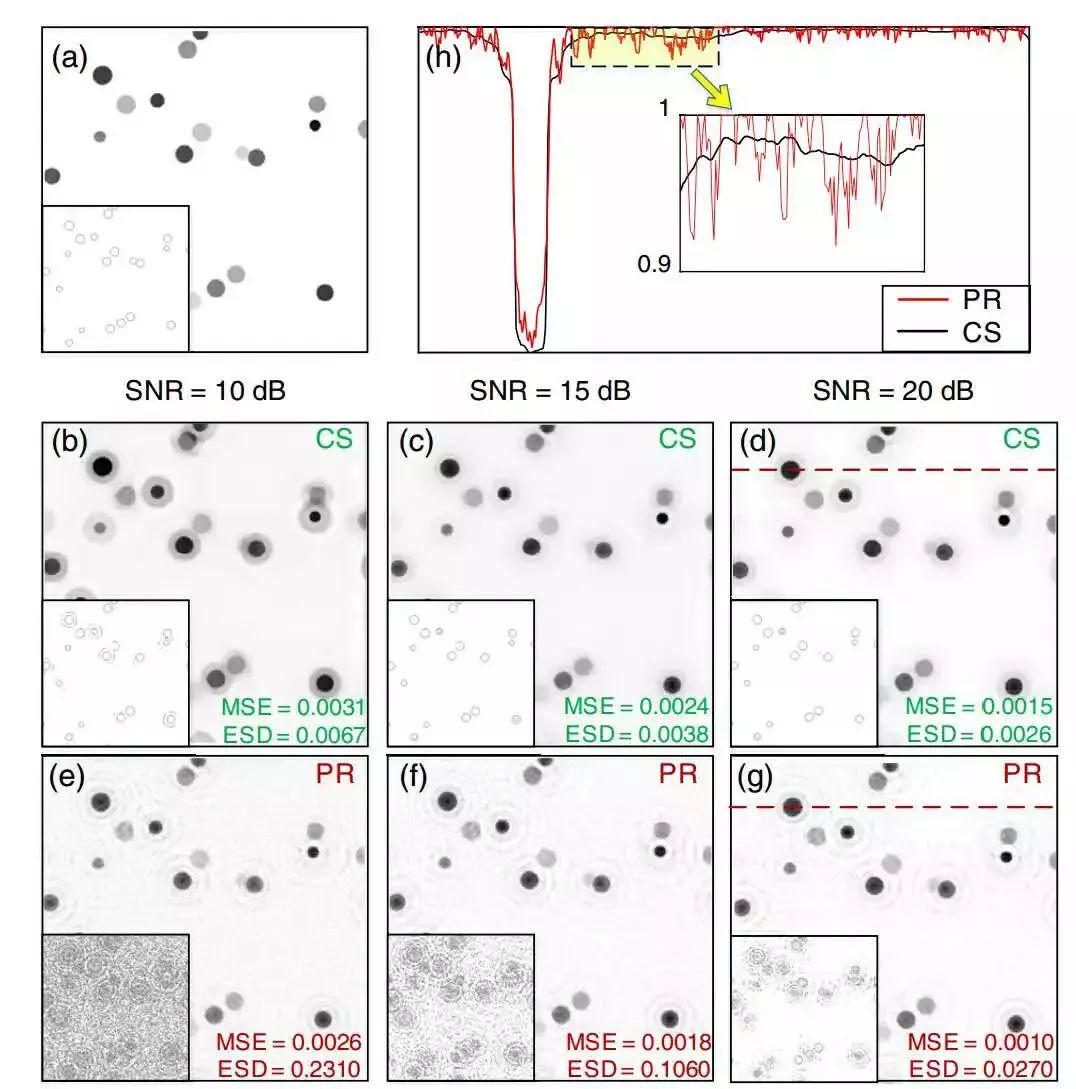
（a）原始图像和边缘矩阵图像；

（b-d）50次迭代后的CS重建和相应的边缘矩阵图像；